FINITE-TEMPERATURE PERTURBATION THEORY FOR THE RANDOM DIRECTED POLYMER PROBLEM
Korshunov S.E., Geshkenbein V.B., Blatter G.

Поступила в редакцию: 25 Апреля 2013

DOI: 10.7868/S0044451013090150

DJVU (118.3K)

PDF (254.6K)

Dedicated to the memory of Professor Anatoly Larkin} We study the random directed polymer problem - the short-scale behavior of an elastic string (or polymer) in one transverse dimension subject to a disorder potential and finite temperature fluctuations. We are interested in the polymer short-scale wandering expressed through the displacement correlator , with δ u (X) being the difference in the displacements at two points separated by a distance X. While this object can be calculated at short scales using the perturbation theory in higher dimensions d > 2, this approach becomes ill-defined and the problem turns out to be nonperturbative in low dimension and for an infinite-length polymer. In order to make progress, we redefine the task and analyze the wandering of a string of a finite length L. At zero temperature, we find that the displacement fluctuations depend on L and scale with the square of the segment length X, which differs from a straightforward Larkin-type scaling. The result is best understood in terms of a typical squared angl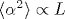e , where 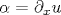, from which the displacement scaling for the segment X follows naturally, . At high temperatures, thermal fluctuations smear the disorder potential and the lowest-order results for disorder-induced fluctuations in both the displacement field and the angle vanish in the thermodynamic limit L → ∞. The calculation up to the second order allows us to identify the regime of validity of the perturbative approach and provides a finite expression for the displacement correlator, albeit depending on the boundary conditions and the location relative to the boundaries.